Game Theory & Halo or, The Tragedy of the Common [Player]

If you’re a guy growing up in the late 90’s or 2000’s, you probably played Halo with your friends, you probably knew how good they were, especially relative to yourself.[1] We are discussing a free for all game mode, where players fight one another without being placed into teams. In Halo, the game mode is called Slayer. For some reason, one of your friends will be very good, they’ll have spent a long time playing these games, or played the campaign on Legendary difficulty, or the game online for days at a time, while being blessed with phenomenal subtle motor controls. For some other reason, there will be a friend that hasn’t played Halo or similar games before and joins you for periodic sessions – they are the bad player. Becoming a good player requires significant investment – most players do not want to pay that cost.

Your friends are also likely to know generally where they sit – meaning the sum of the individuals playing actually generates a pretty good intelligent network and pyramid of relative strength. For simplicity’s sake, let’s put everyone into a grouping of bad, normal, and good players. Once a very good player is introduced, they will dominate the game. Let’s assume:

· There’s only one good player that dominates the game.

· Everyone knows each other’s strengths.

· Everyone can identify who everyone else is (except maybe the bad player, who can’t pick out that kind of detail yet).

· There are only points to be earned, there are no penalties for dying (except one’s pride).

· There are no other ways to win points except to defeat an opponent.

there’s usually a bit of a variation when you play against your friends in free for all, such that,

· N(μ,σ)

· A bad player earns: N(2,1)

· A normal player earns N(18,4)

· A good player earns N(25,2) [2]

where the mean (μ) = the number of points, or kills made, and 25 points is how much it takes to win the match.

On average, a good player will generally win, while a normal player might win every once in a while. I am confident that actual data would prove this a relatively fit model for actual performance. If we assume that these points also transfer to the probability of success on each encounter, we can generate a payoff matrix. There is a different probability of success based on who one encounters.

Table 1: Probability of Success

P(Row Player, Column Player)	Good Player	Normal Player	Bad Player
Good Player	-	(90%, 10%)	(99%, 1%)
Normal Player	(10%, 90%)	(50%, 50%)	(95%, 5%)
Bad Player	(1%, 99%)	(5%, 95%)	(50%, 50%)

We can translate these probabilities into points with each encounter, because each encounter leaves the opportunity for 1 point:

Table 2: Expected Payoffs

Payoff: (Row, Col)	Good Player	Normal Player	Bad Player
Good Player	-	(0.9, 0.1)	(0.99, 0.01)
Normal Player	(0.1, 0.9)	(0.5, 0.5)	(0.95, 0.05)
Bad Player	(0.01, 0.99)	(0.05, 0.95)	(0.5, 0.5)

How do you play as different players?

If you’re the best player, your odds of beating any of your friends are generally pretty good. The best player’s strategy is simply to kill as many people as possible, as fast as possible. The only real chance at losing the best player has is because of time: if your friends kill each other at a faster rate than you kill them, one of them might get enough points to win.

If you’re the worst player, you’re honestly just trying to have a good time and your good time is being interrupted all too fast the entire game.

If you’re in the general pack your thought process is more difficult. Do you try to avoid the best player and hunt everyone else, where you have better odds of winning? Do you try to hit everyone at an equal rate and die more often when you meet the best player? Do you just hunt the bad player wherever he spawns? Do you start camping as a sniper and anger your friends? The dominant strategy is clearly to try and kill only the worst player. But it’s hard to find them, and you keep running into everyone on your merry way to kill your lost friend. In other words, the expected payoff per encounter is excised from any strategy because one cannot manipulate who one encounters. The expected payoff can be multiplied by the probability of the encounter.

If everyone moved at the same speed and there are N players (including the best and worst player), then the probability of encountering each individual is the following (in consideration of removing oneself from the possible encounter):

Table 3: Baseline Probability of Encounter

Probability (Row, Col)	Good Player	Normal Player	Bad Player
Good Player	0	N - 2 / N - 1	1 / N - 1
Normal Player	1 / N - 1	N - 3 / N - 1	1 / N - 1
Bad Player	1 / N - 1	N - 2 / N -1	0

The probability needs to be adjusted because everyone does not move at the same speed. When players are respawned, they are spawned outside of the main area of conflict. Given that experienced players know maps and act efficiently to rack up points, they will be relatively quick. In contrast bad players will be less efficient and more likely to wander aimlessly. We have to adjust the probability of encounter upwards for good players and downwards for bad players.

Table 4: Probability of Encounter Factoring Player Skill

Probability (Row, Col)	Good Player	Normal Player	Bad Player
Good Player	0	A (N - 2) / N - 1	AB / N - 1
Normal Player	A / N - 1	N - 3 / N - 1	B / N - 1
Bad Player	AB / N - 1	B ( N - 2) / N - 1	0

Where A and B represent the adjustment to the probability that players encounter the good and bad player, respectively, and A > B > 0.

Everyone is therefore likely to try and kill everyone but the bad player will be less likely to be encountered and the good player will be more likely to be encountered. To be clear, one is not actively searching for a certain player as a strategy, one simply encounters other players. Though the bad player will be killed often, it will be more difficult to encounter them. Playing the game normally will result in high chances of encountering the good player and relatively low chances to encounter bad players. In other words, it will be extremely difficult to just attack the weak guy. As a result, the best player is almost certain to win – hence the initial probability distributions as a long-term outcome.

______

There’s a catch. During free for all matches, three-way fights occur. One, for instance, walks into a room at the same time as a foe walks in, and there’s a third foe already in the room. Or perhaps one is fighting a foe and another foe swoops in on a Banshee (an aircraft) and joins the fracas. These three-way fights make the game more interesting because they provide an opportunity to realign the expected payoffs. To be clear, these three-way matchups occur pretty often in many of these free-for-all games. When one finds oneself in this situation, who does one attack, and why? For the first time, a strategic decision can be made.

Combining fires in these games is not a simple addition of probabilities; a player receiving concentrated fire is much more likely to lose, even throwing a bad player into the mix can alter probabilities if only because they distract another player – perhaps just long enough for them to be demolished. We must therefore construct a new matchup payoff. For simplicity let’s call these happenstances of combined fires a “team.”

Table 5: Probability of "Team" Success

P(Row, Col)	Good Player	Normal Player	Bad Player
B. Player + G. Player	N/A	(95%, 5%)	N/A
B. Player + N. Player	(25%, 80%)	(65%, 35%)	N/A
N. Player + N. Player	(65%, 35%)	(90%, 10%)	(99%, 1%)
N. Player + G. Player	N/A	(99%, 1%)	(99%, 1%)

Since the expected payoff is directly based on the probability of success, we can dispense with calculating it again. One notices several interesting things. First, the bad player is still out of luck. Second, the best player still generally dominates. More importantly however, the normal players now have a much higher chance to defeat the best player than they did on their own. Lastly, a normal player still has a better outcome from “teaming up” with the best player against a normal player than by “teaming up” with a normal player against the best player. The dominant strategy for normal players is therefore to attack each other, and avoid shooting the best player. Of course once the three-way engagement has concluded, each player will continue fighting one another – reverting the odds back to initial one-on-one engagement (where the best player dominates). Both normal players are therefore essentially sentenced to doom as a result of following their dominant strategy. Furthermore, the best player will receive less fire overall since it will be more difficult to defeat them in the first place – giving the best player even more of an advantage.

We can also visualize a three-way fight in terms of a decision tree. For simplicity, we remove the bad player, and the three-way matchup against another normal player, multiply the expected payoff by the probability of success and round to the nearest whole number. The score of beating the good player (expected value of 1) is divided between the normal players – yielding 0.5 each. The same could be done for a split kill between a normal player and a good player, but the good player is far more likely to earn the kill than their erstwhile ally.

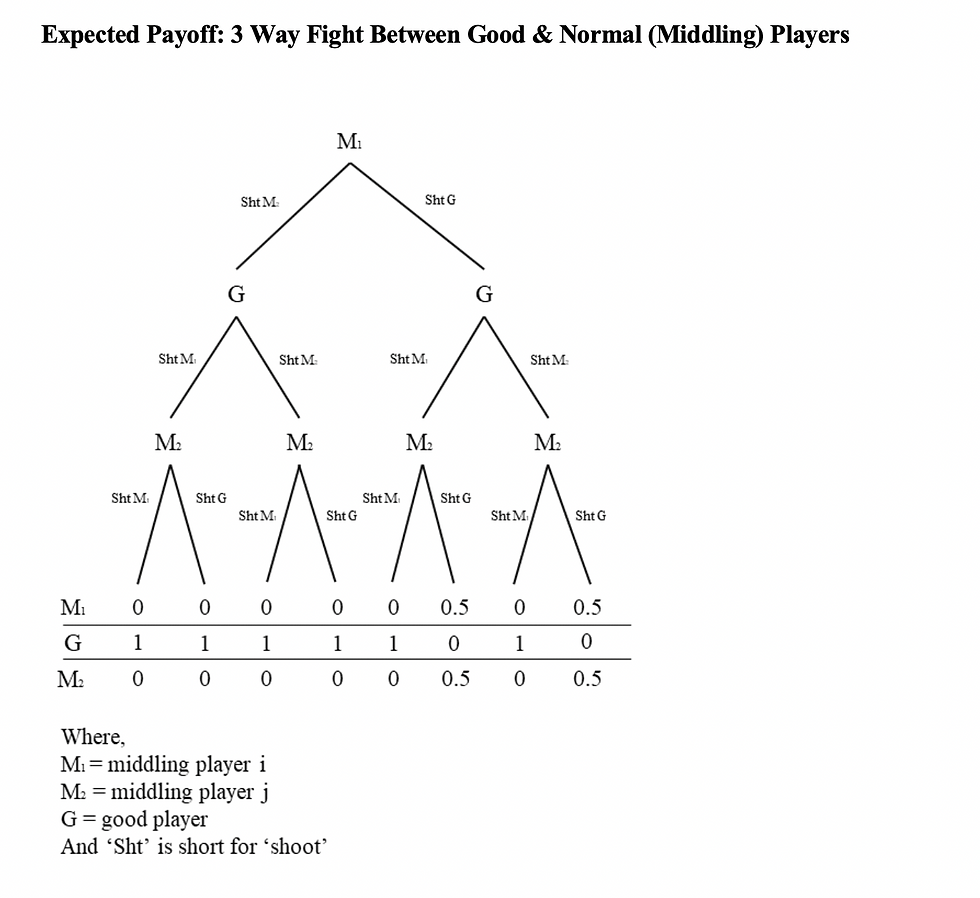
A different way to look at the expected success is the implied risk. Lower expected success implies higher risk. Building a decision tree showing implied risk showcases why, if players are risk averse, they would always want to ally with the good player against a normal player, even though their expected payoffs are generally worse.

The issue is that this is not the socially optimal approach. The socially optimal approach is that each player has a chance to win (except maybe the bad player, because what kind of world do we live in if the bad player has a shot). Consider if these three-way engagements occurred only twice in one game, and assume both engagements were completely won by a normal player (they defeat the best player and another player). The normal player now has four points, while the best player has zero new points. Considering that the mean number of expected points per normal player was 18 with a standard deviation of 4, the normal player has a much higher chance of winning the game. What would be socially optimal is therefore that normal players consistently focus their fires on the good player, reduce the probability that the good player earns a point while guaranteeing that each normal player earns 0-2 points. A slight marginal advantage to each normal player in the game would not only boost their total point counts but also increase the time the game is played. When considering again that the best player is in a race against time, this is yet another benefit to normal players.

Implications

This essay is all fun and games until one realizes this analysis can be applied to other ‘free-for-all’ environments. For instance, interstate behavior is typically described as anarchic realism. States can also be assumed to have a pretty good understanding of each other’s relative strengths. In the short term therefore, we should expect weaker states to not ally with one another but to ally with strong states. The problem is that strong states get stronger and it’s only a matter of time before they dominate or consume their weaker counterparts. Say we were discussing colonialism – would a native tribe or state ally with their legacy rivals against European encroachment, or would they rather make a temporary alliance with the Europeans and crush their rivals – only to get steamrolled later themselves?

Just as in the prisoner’s dilemma, a pact must be made between middling players to agree to focus fires on the best player. They must however first come to the realization that this would be a socially optimal outcome. When dealing with socially optimal outcomes however, one is reminded of the difficulty in paying for public goods or paying for negative externalities. In both circumstances, parties covered by public goods or parties that generate negative externalities are incentivized to not follow agreements to sustain public goods or reduce negative externalities. Any intransigent behavior can doom the capability to deal with these problems. Observing that a pact is necessary in the first place should not be dismissed as a small barrier: for instance it took humanity a long time to determine that we caused global warming (still denied by some self-serving parties); distrust of the government causes some members of society to form their own militias, undermining the potentially more effective public good of a national cohesive standing army.

Another insight can be gleaned from the assumptions made to discuss this piece: that one must know the relative strength of the players involved with relatively high amounts of certainty. In the absence of this knowledge, it will not be possible for players to even consider aligning themselves against a stronger opponent. Players may be able to develop heuristics to determine if the opponent they encountered is better than themselves – but in first person shooters typically there is little time to gather information once an encounter has been made. Likewise in interstate competition, it is necessary for countries to have a good understanding of one another’s relative strengths enabling the creation of balancing coalitions to escape hegemony.

[1] Note this discussion can be applied to other video games played with friends but the author is excessively experienced in playing Halo, having grown up in the late 90’s and 2000’s. [2] Assume of course there is a cap at 25, meaning the standard deviation of points for the good player is applicable downwards only.